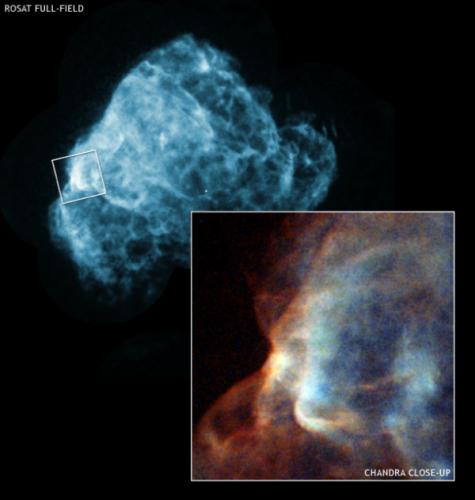
Puppis A: A supernova remnant about 7,000 light years from Earth
Caption: Chandra's three-color image (inset) of a region of Puppis A (blue ROSAT wide-angle image) reveals a cloud being torn apart by a shockwave produced by a supernova explosion. This is the first X-ray detection of such a process in an advanced phase. In the inset, the blue vertical bar and the blue fuzzy ball or cap to the right show how the cloud has been spread out into an oval-shaped structure that is almost empty in the center. Understanding how shock waves interact with clouds is important for answering key questions such as the role supernovas play in heating interstellar gas and triggering the collapse of large interstellar clouds to form new generations of stars.
Scale: ROSAT image is 88 arcmin across; Chandra image is 8 arcmin across
Chandra X-ray Observatory ACIS Image
|