For Release: November 15, 2006
CXC RELEASE 07-06
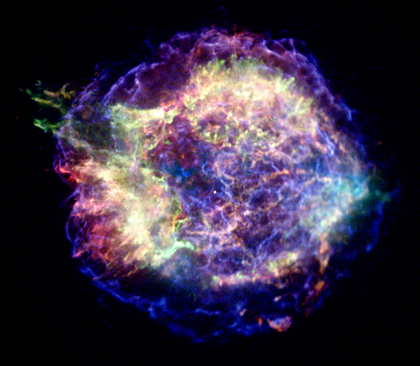
New clues about the origins of cosmic rays, mysterious high-energy particles that bombard the Earth, have been revealed using NASA's Chandra X-ray Observatory. An extraordinarily detailed image of the remains of an exploded star provides crucial insight into the generation of cosmic rays.
For the first time, astronomers have mapped the rate of acceleration of cosmic ray electrons in a supernova remnant. The new map shows that the electrons are being accelerated at close to the theoretically maximum rate. This discovery provides compelling evidence that supernova remnants are key sites for energizing charged particles.
The map was created from an image of Cassiopeia A, a 325-year-old remnant produced by the explosive death of a massive star. The blue, wispy arcs in the image trace the expanding outer shock wave where the acceleration takes place. The other colors in the image show debris from the explosion that has been heated to millions of degrees.
"Scientists have theorized since the 1960s that cosmic rays must be created in the tangle of magnetic fields at the shock, but here we can see this happening directly," said Michael Stage of the University of Massachusetts, Amherst. "Explaining where cosmic rays come from helps us to understand other mysterious phenomena in the high-energy universe."
Examples are the acceleration of charged particles to high energies in a wide variety of objects, ranging from shocks in the magnetosphere around Earth to awesome extragalactic jets that are produced by supermassive black holes and are thousands of light years in length.
Scientists had previously developed a theory to explain how charged particles can be accelerated to extremely high energies - traveling at almost the speed of light - by bouncing back and forth across a shock wave many times.
"The electrons pick up speed each time they bounce across the shock front, like they're in a relativistic pinball machine," said team member Glenn Allen of the Massachusetts Institute of Technology (MIT), Cambridge. "The magnetic fields are like the bumpers, and the shock is like a flipper."
In their analysis of the huge data set, the team was able to separate the X-rays coming from the accelerating electrons from those coming from the heated stellar debris. The data imply that some of these electrons are accelerated at a rate close to the maximum predicted by theory. Cosmic rays are composed of electrons, protons, and ions, of which only glow from electrons is detectable in X-rays. Protons and ions, which constitute the bulk of cosmic rays, are expected to behave similarly to the electrons.
"It's exciting to see regions where the glow produced by cosmic rays actually outshines the 10-million-degree gas heated by the supernova's shock waves," said John Houck, also of MIT. "This helps us understand not only how cosmic rays are accelerated, but also how supernova remnants evolve."
As the total energy of the cosmic rays behind the shock wave increases, the magnetic field behind the shock is modified, along with the character of the shock wave itself. Researching the conditions in the shocks helps astronomers trace the changes of the supernova remnant with time, and ultimately better understand the original supernova explosion.
NASA's Marshall Space Flight Center, Huntsville, Ala., manages the Chandra program for the agency's Science Mission Directorate. The Smithsonian Astrophysical Observatory controls science and flight operations from the Chandra X-ray Center, Cambridge, Mass.
Additional information and images are available at:
MEDIA CONTACTS
Steve Roy
Marshall Space Flight Center, Huntsville, Ala.
(Phone: 256/544-6535)
Megan Watzke
Chandra X-ray Center, Cambridge, Mass.
(Phone: 617/496-7998)